在数字、模拟电路中，我们经常遇到带宽（BW）和采样频率（Fs）这两个参数，如何理解呢？我们通过下面一个应用实例来解释说明一下。

第一部分 带宽BW的意义                                             

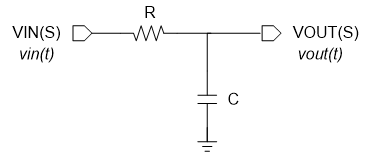
图（一） 电阻R和电容C构成的一阶低通滤波器

以电阻R和电容C构成的低通滤波器系统为例，如图（一）所示，根据自控原理的理论基础可知，其传递函数定义为：

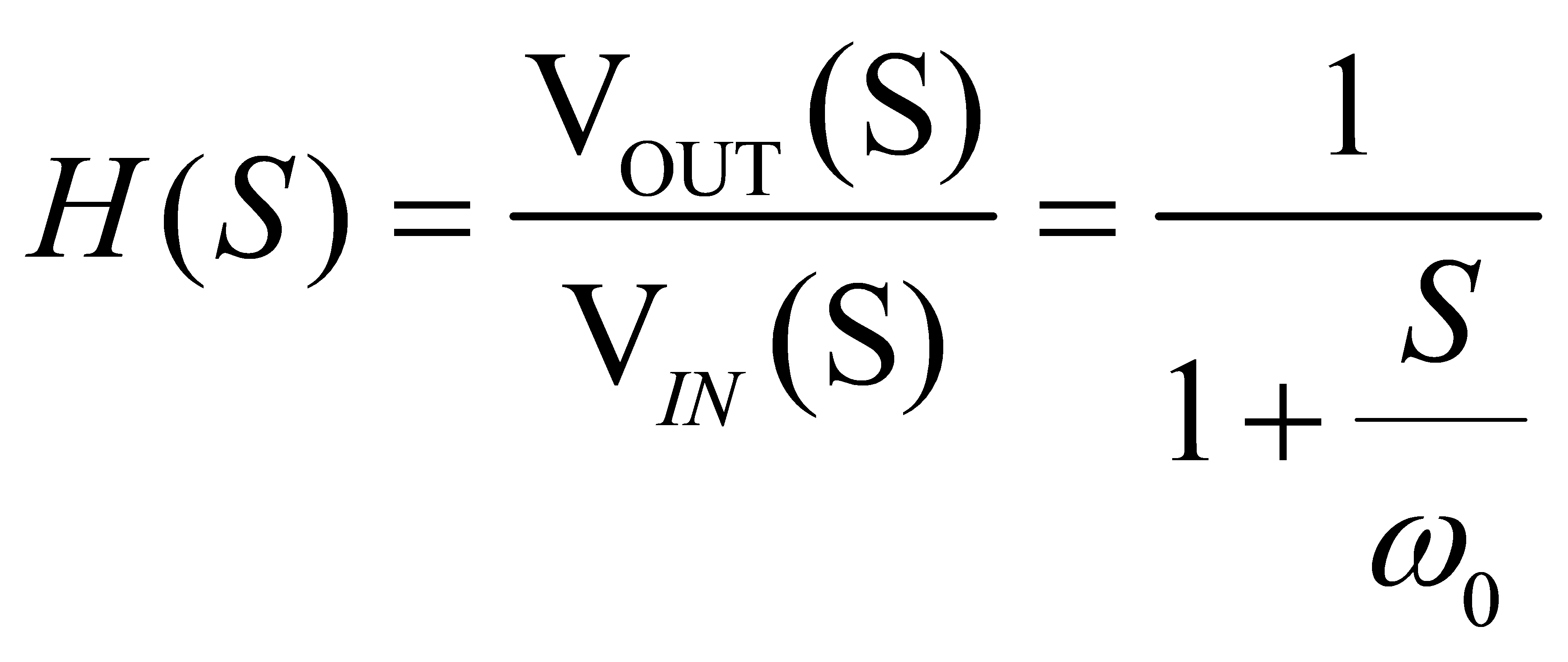       （1）

其中，，为角频率（单位是弧度/秒）。角频率和通常意义的频率（单位为Hz）之间的关系是：。

一阶低通滤波器的幅频特性Magnitude和相频特性Phase分别为：

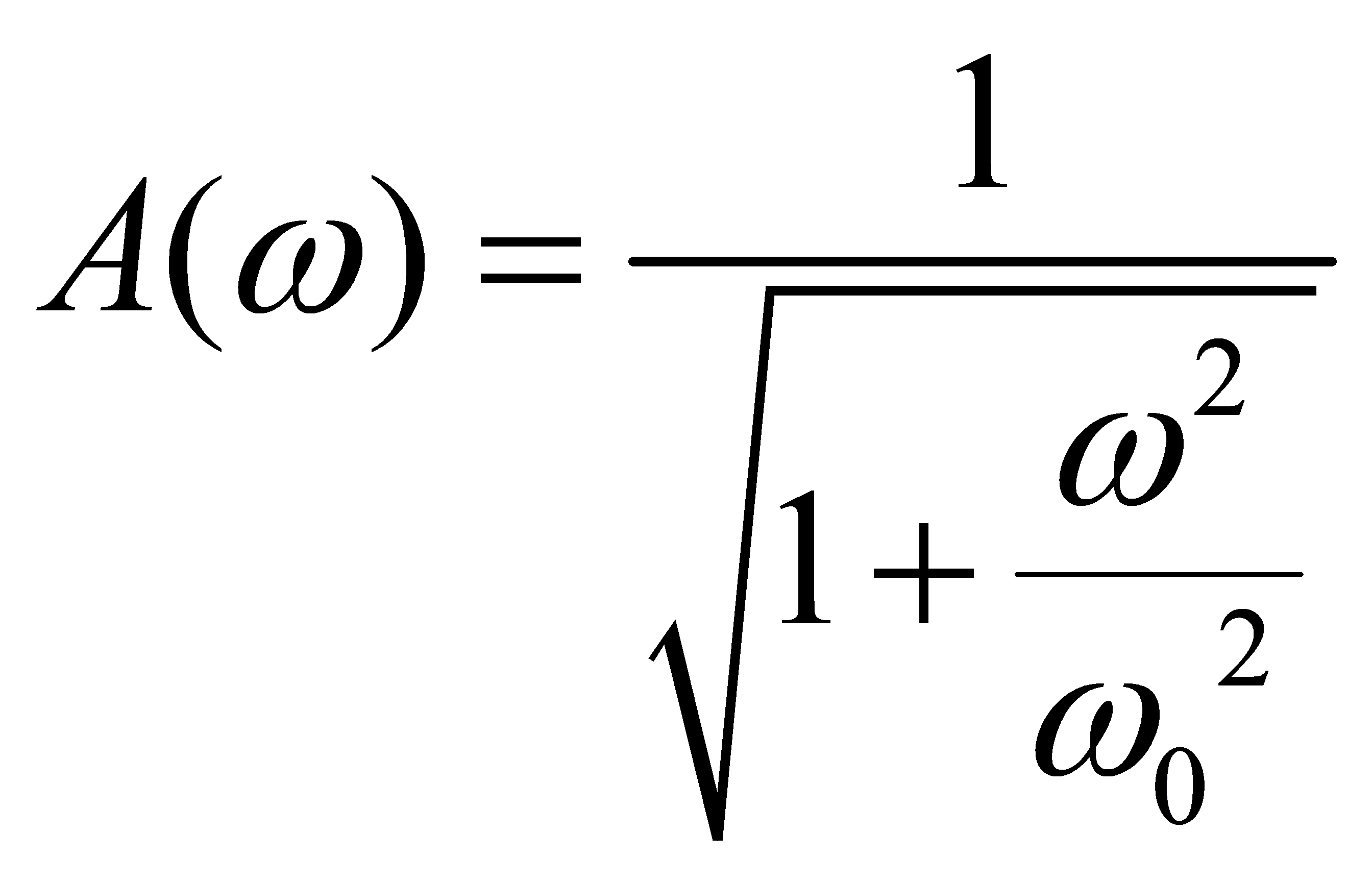                   （2）

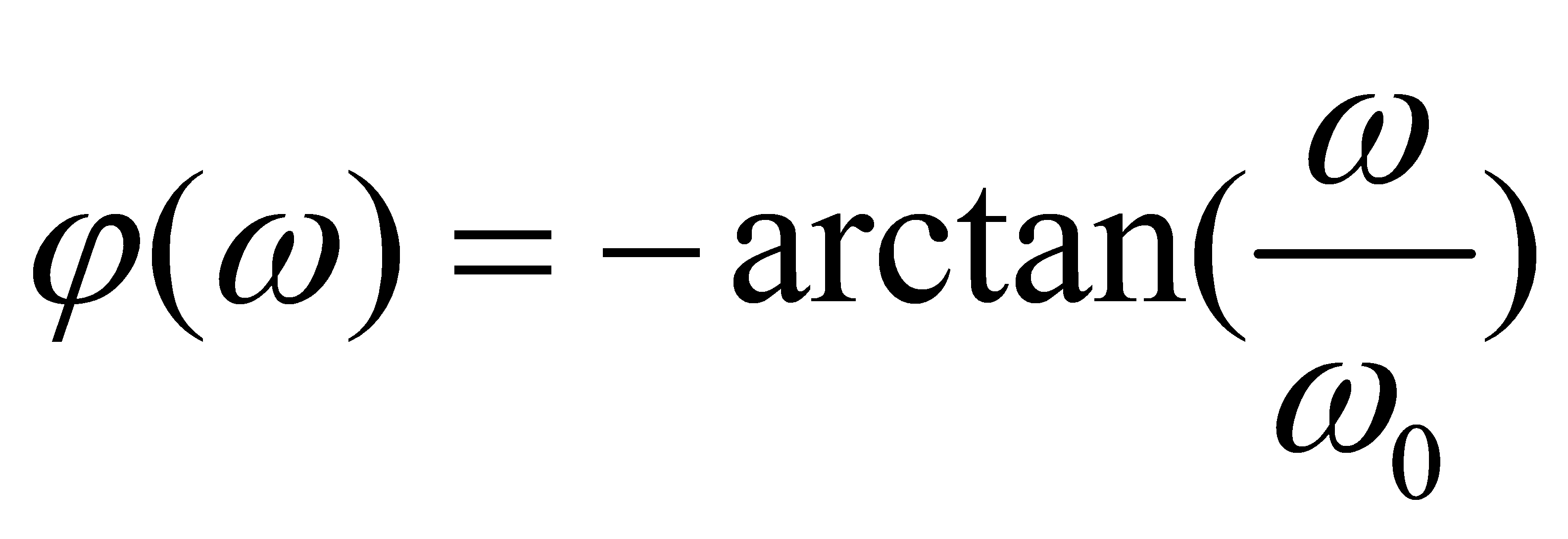                    （3）

由公式（2）和（3）不难得出如下结论：

（a）     当时，，，即信号幅度衰减为0.707倍（-3dB），相移-45°

（b）    当时，，，即信号幅度几乎没有衰减，相移-5.7°

（c）     当时，，，即信号幅度衰减为0.1倍（-20dB），相移-84.3°

习惯上，将-3dB信号幅度衰减所对应的频率，定义为系统的带宽；以图（一）所示一阶低通滤波器为例，其带宽为。

第二部分 系统带宽BW对不同输入信号响应的影响

这里还是以一阶低通滤波器为模型进行说明（计算过程有兴趣请参考自控原理等相关书籍），当输入信号为：

（1）     正弦信号

即：                    （4）

则：                   （5）

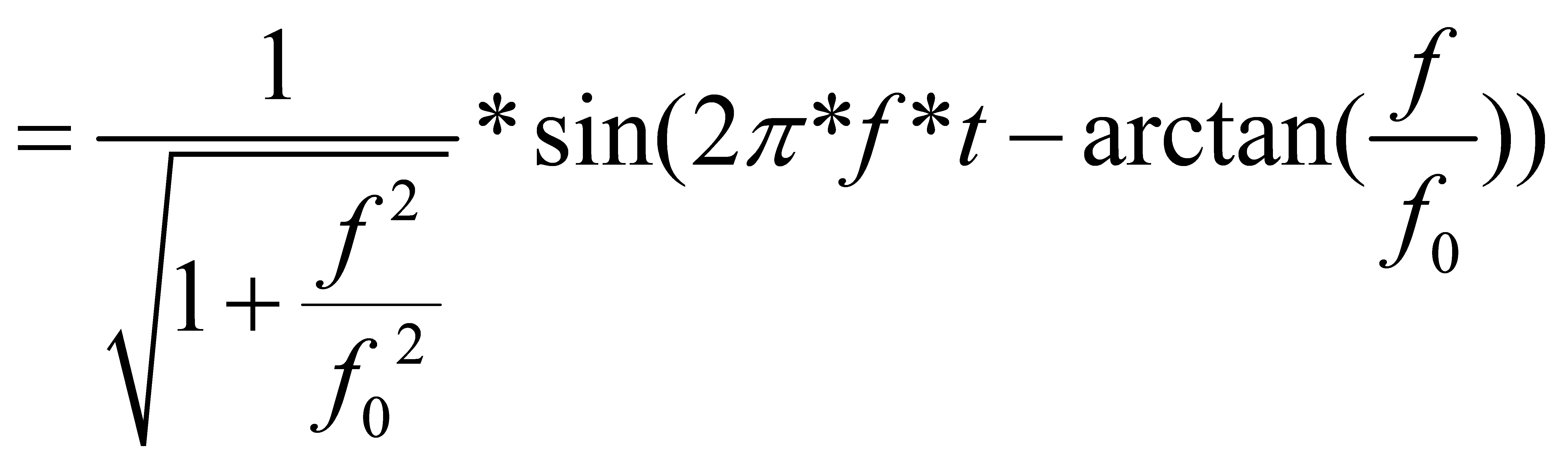
为了方便起见，将一阶低通滤波器的带宽归一化，即令，对于相同幅度不同频率的输入信号，其输入/输出关系如图（二）所示，可以看到：随着正弦输入信号的频率越来越高，一阶低通滤波器输出的幅值越来越小，相移越来越大。

图（二） 一阶低通滤波器对不同频率正弦输入信号的响应

（2）     阶跃信号

即

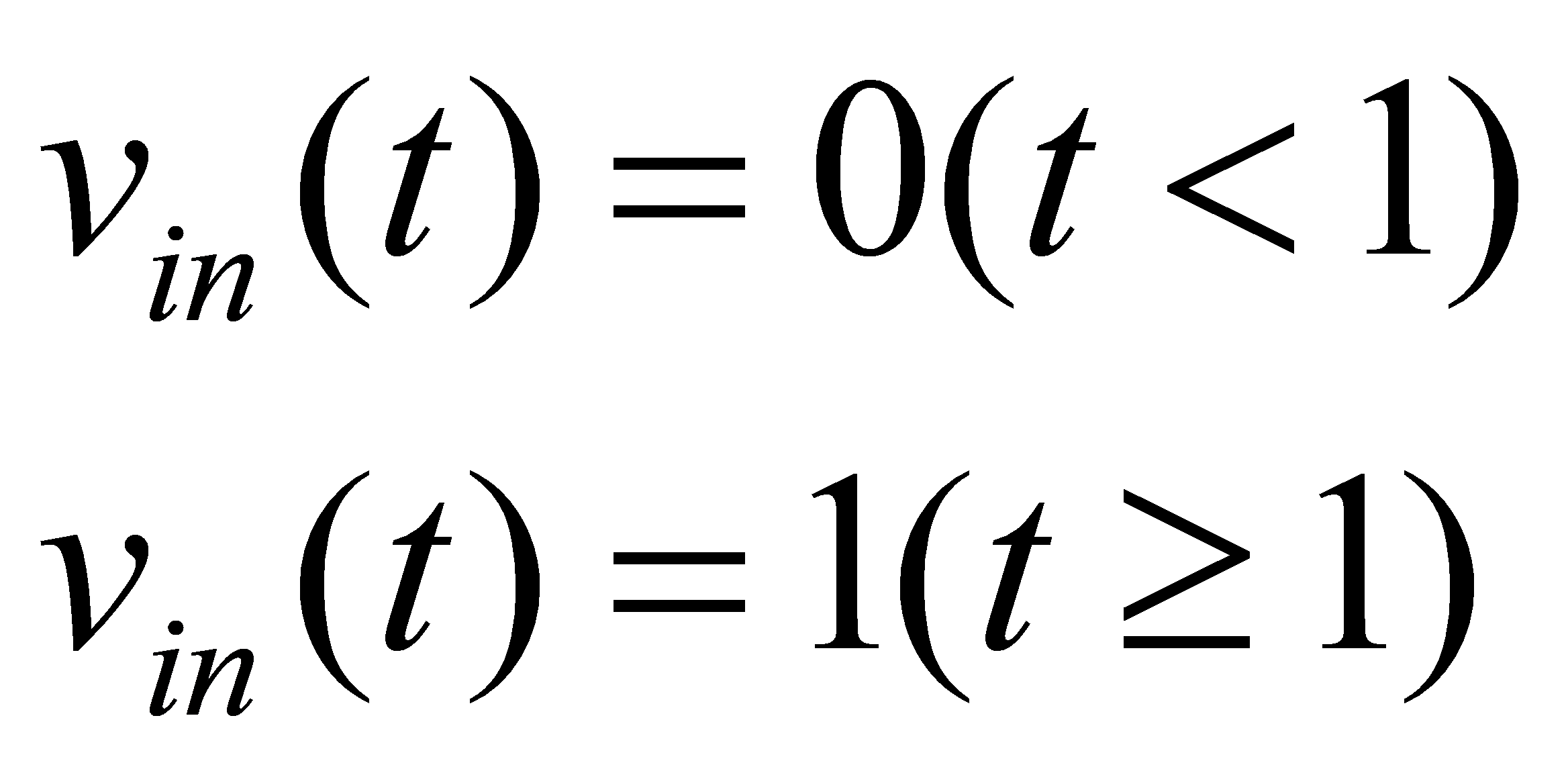                                                        （6）

则

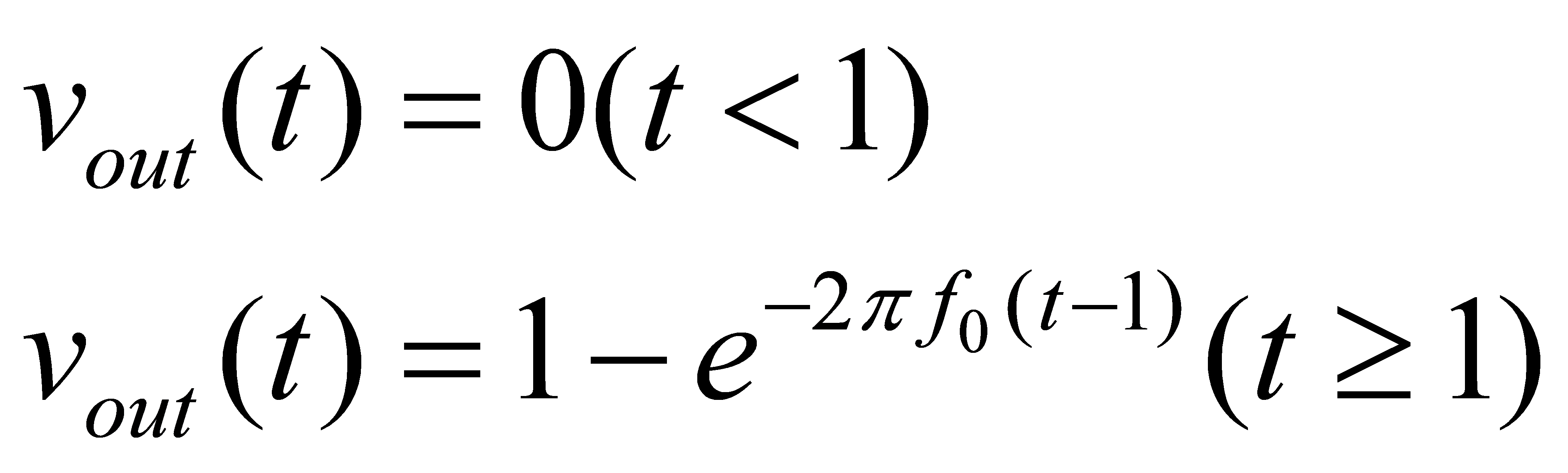                                     （7）

从公式（7）可以看出， settle到90%的幅值所需的时间是：

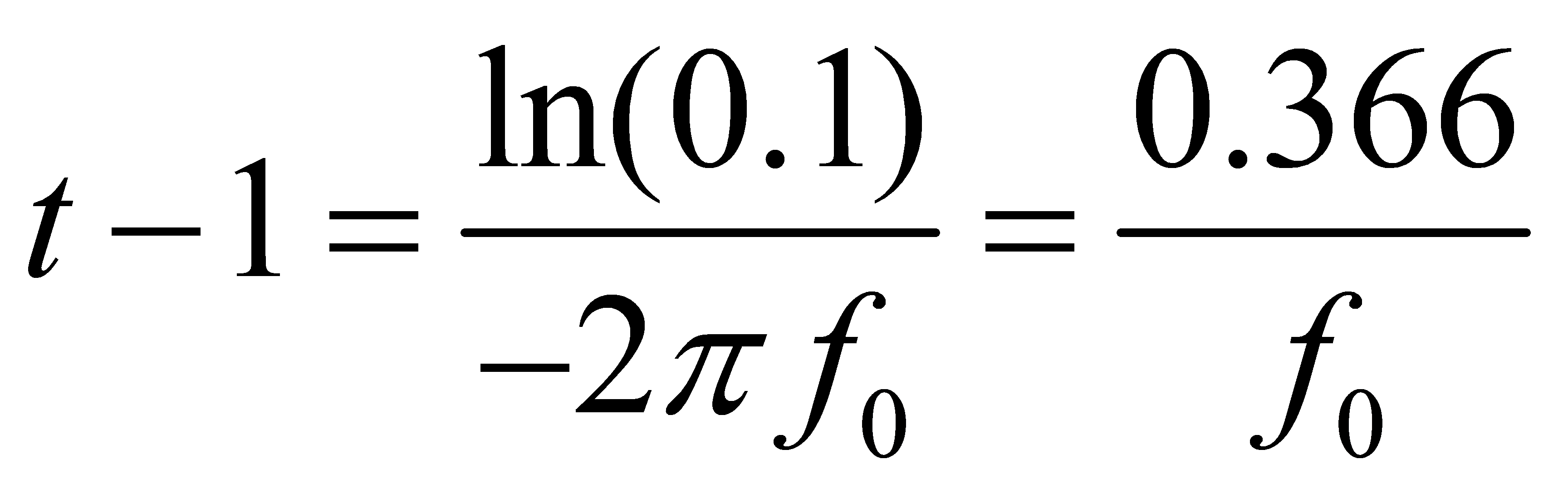                                             （8）

因此一阶低通滤波器的带宽越大，则系统对输入信号的响应越快，其输入/输出关系如图（三）所示，

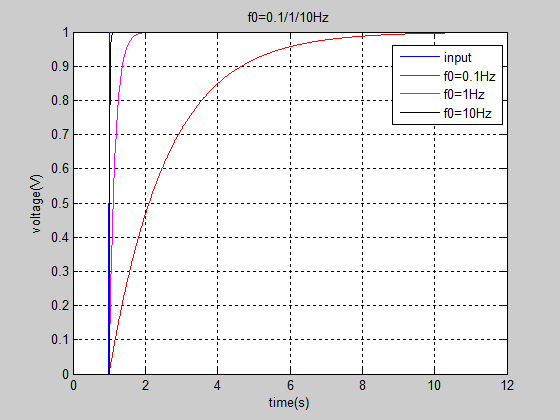
图（三） 不同带宽的一阶低通滤波器对阶跃信号的响应

（3）     应用实例

以上分析均基于一阶低通滤波器模型，对于高阶滤波器模型的带宽及其响应，有兴趣的读者可以参考自控原理相关教材，这里不做赘述。

MagnTek公司MT910x系列线性霍尔产品，可以用一阶低通滤波器模型来近似，如图（四）所示为典型应用框图：MT910x检测外界磁场信号，并将其转化为电压信号，客户可以用ADC对输出电压信号进行采样并将其转化为数字信号，以便后续进行更为复杂的数字信号处理。

这里，从到之间便可以用一个带宽为30KHz的一阶低通滤波器模型来近似（需要在公式（1）的分母上乘以MT910x的灵敏度）。有兴趣的读者可以推导下针对不同外界输入磁场，MT910x的响应。

图（四） MT910x系列线性霍尔产品的典型应用框图

第三部分 带宽和采样率的关系

如图（五）所示为一个典型的采样系统：模拟输入电压信号Vin经过模数转换器（ADC）采样/量化得到Dout，Dout经过数模转换器（DAC）得到模拟输出电压信号Aout，Aout经过理想低通滤波器（LPF）滤波，便可以得到平滑后的模拟电压信号Fout。采样定律描述的便是满足什么样的条件，Fout 100%等于Vin。

图（五） 典型的采样系统

根据采样定律的理论可知，要想不失真地对模拟信号进行采样，需要满足条件：采样频率Fs大于等于信号带宽的2倍。

下面就来定性的分析一下采样定律。在此之前先明确一个概念：根据信号与系统的相关理论，任何一个信号都有时域和频域两种表示方式，这两种表示方式完全等价，并可以运用傅里叶变换和反傅里叶变换相互转化。也就是说，一个信号时域波形确定了，其频谱图也就确定了，反之亦然。

（1）     采样率大于信号带宽2倍

如图（六）所示为采样率大于信号带宽2倍时，图（五）所示采样系统各个节点处的信号，左边的图横坐标是时间，纵坐标是幅值，表示该信号的时域波形；右边的图横坐标是频率，纵坐标是幅值，表示该信号的频谱图。

l  对于信号带宽为BW_sig的模拟信号Vin，经过ADC采样/量化后，可以得到数字信号Dout；

l  Dout在时间和幅度上均为离散值，并且其频谱就是Vin的频谱在Fs整数倍（0,1,2,3...）处镜像叠加的组合；如果ADC的采样频率Fs大于信号带宽BW_sig的2倍，则Dout的频谱如图所示；

l  接下来的DAC仅仅是将数字信号转换为模拟信号，并不改变信号的形状，因此Aout和Dout的时域波形及频谱图均一致；

l  理想低通滤波器的作用是将频率小于其带宽的信号无衰减通过，将频率大于其带宽的信号完全抑制。因此，如果设置滤波器带宽BW=Fs/2，Aout经过滤波器后得到Fout的频谱与Vin的频谱形状完全一样，则Fout和Vin的时域波形也完全一样；

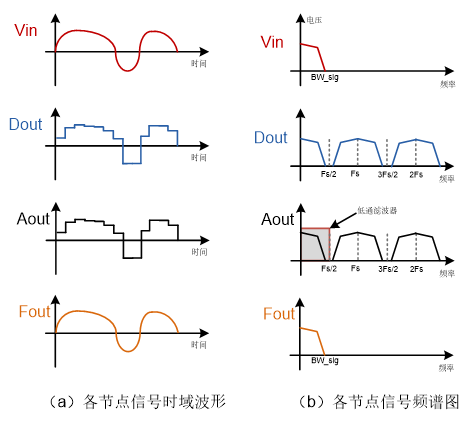
图（六） 采样系统中采样率大于信号带宽2倍时各个节点的信号

       从上面分析可知：当采样率大于信号带宽的2倍时，输入信号Vin经过采样系统后可以被100%还原，信息没有发生丢失。

（2）     采样率小于信号带宽2倍

如图（七）所示为采样率小于信号带宽2倍时，图（五）所示采样系统各个节点处的信号。区别在于：

l  Dout的频谱是Vin的频谱在Fs的整数倍（0,1,2,3...）处镜像叠加的组合；由于Fs/2<BW_sig，因此在Fs/2的奇数倍（1,3,5,7...）附近的频谱是相邻两个镜像频谱的叠加，此叠加过程被称为“混频”，并且不可逆；

l  一旦混频现象发生，无论用何种滤波器都无法使频谱复原，如图所示设置滤波器带宽BW=Fs/2，Aout经过滤波器后得到Fout的频谱与Vin的频谱已经不再一样了，则Fout相对于Vin的时域波形也发生了畸变；

补充一下：混频过程既能导致信号畸变，也能将信号上叠加的高频噪声“折叠到”带宽内。

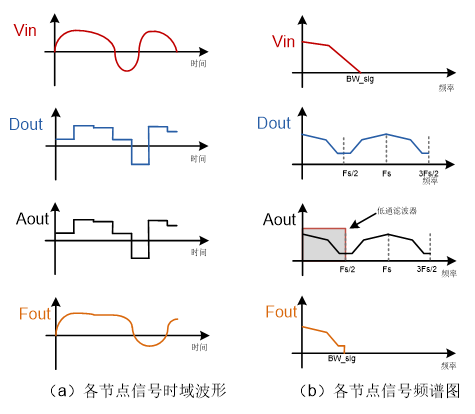
图（七） 采样系统中采样率小于信号带宽2倍时各个节点的信号

从上面分析可知：当采样率小于信号带宽的2倍时，输入信号Vin经过采样系统后无法100%还原，即信息发生丢失。

（3）     应用实例

在现实中，理想的低通滤波器是无法实现的，由于实际的低通滤波器过渡带无法做到无限窄，如图（八）所示，因此为了保证不发生混频，采样率一般会远远高于2倍信号带宽。

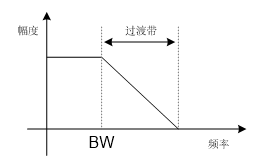
图（八） 实际的低通滤波器存在过渡带

       以图（四）MT910x的典型应用为例，MT910x输出信号的带宽为30KHz，为了避免混叠现象的发生，充分利用MT910x的性能，建议将ADC的采样率设置在10倍信号带宽以上，即Fs>300KHz。

作者：北极星  出处：麦歌恩官网